Laboratory 5

The aim of this laboratory session is to reinforce the concepts associated with the Fourier Transform. This will involve constructing filters directly in the frequency domain in order to implement some image enhancement techniques.

Constructing Filters in the Frequency Domain

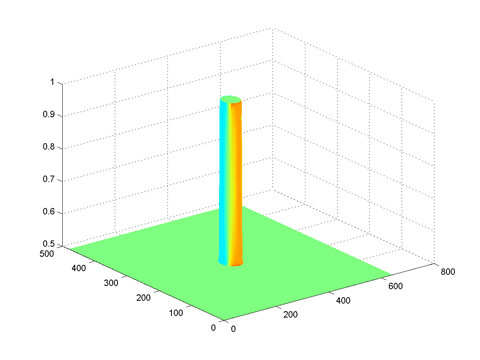
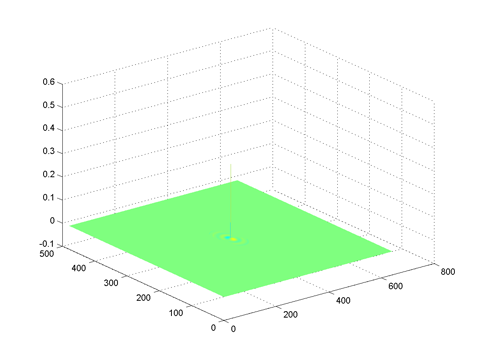
highboostfft = highboostfilter(size(im), 0.05, 50, 0.5) Frequency domain	Spatial domain	highboost filter blurs the image
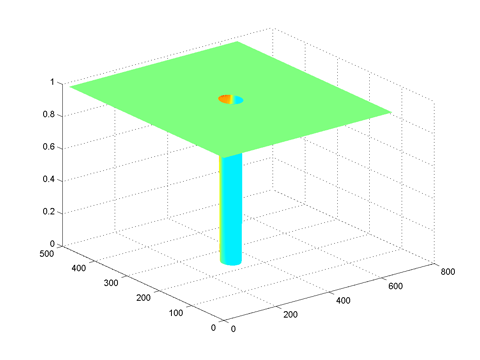
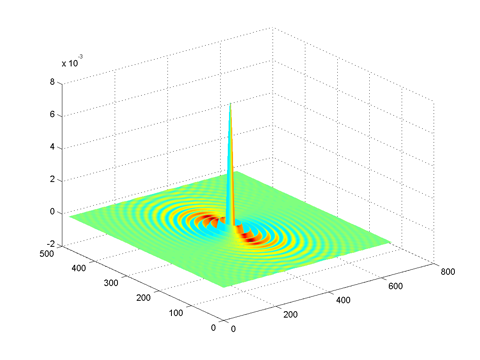
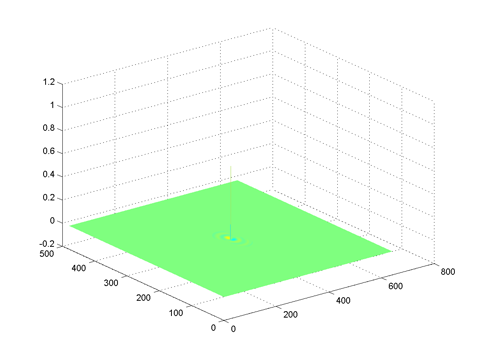
highpassffthigh = highpassfilter(size(im), 0.05, 50) Frequency domain	Spatial domain	high order highpass filter creates a rippling effect
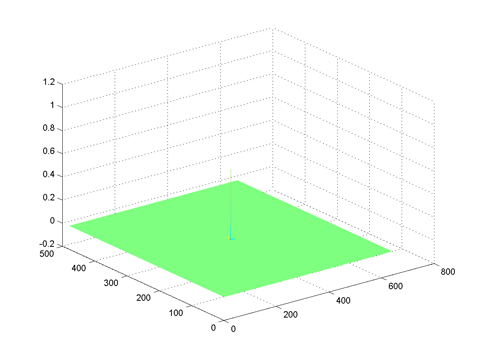
highpassfftlow = highpassfilter(size(im), 0.05, 1) Frequency domain	Spatial domain	low order highpass filter defines the edges
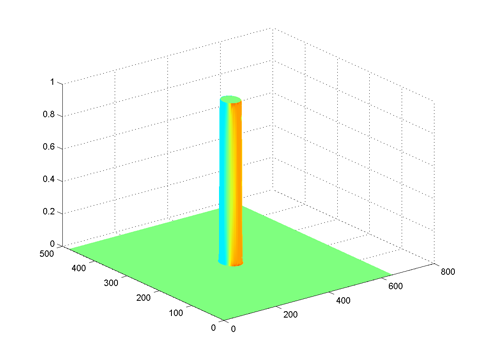
lowpassffthigh = lowpassfilter(size(im), 0.05, 50) Frequency domain	Spatial domain	high order lowpass filter creates a blurred ripple effect
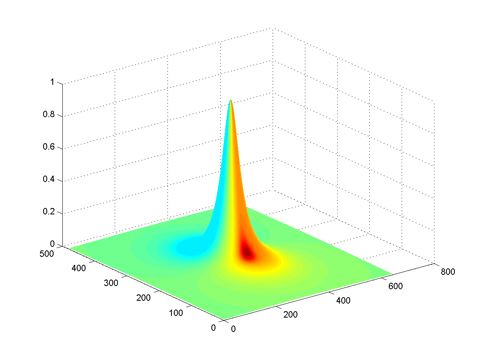
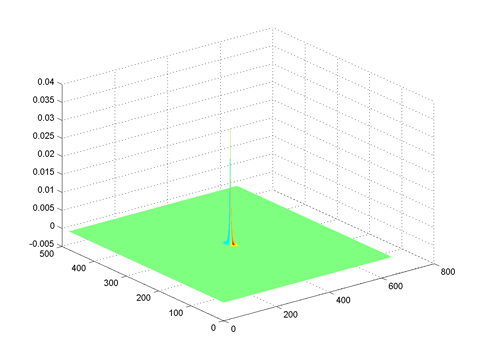
lowpassfftlow = lowpassfilter(size(im), 0.05, 1) Frequency domain	Spatial domain	low order lowpass filter creates a blurred effect

Listing of the code used to create the above images:

im = imread('d:\comp vision\images\travis.jpg');
im = rgb2gray(im);

lowpassffthigh   = lowpassfilter(size(im), 0.05, 50);
highpassffthigh  = highpassfilter(size(im), 0.05, 50);
highboostfft     = highboostfilter(size(im), 0.05, 50, 0.5);
lowpassfftlow    = lowpassfilter(size(im), 0.05, 1);
highpassfftlow   = highpassfilter(size(im), 0.05, 1);

imfft = fft2(im);

surfl(fftshift(lowpassffthigh)), shading interp;
print -dpng lowpassffthighfreq.png
surfl(fftshift(highpassffthigh)), shading interp;
print -dpng highpassffthighfreq.png
surfl(fftshift(highboostfft)), shading interp;
print -dpng highboostfftfreq.png
surfl(fftshift(lowpassfftlow)), shading interp;
print -dpng lowpassfftlowfreq.png
surfl(fftshift(highpassfftlow)), shading interp;
print -dpng highpassfftlowfreq.png

surfl(fftshift(real(ifft2(lowpassffthigh)))), shading interp;
print -dpng lowpassffthighspac.png
surfl(fftshift(real(ifft2(highpassffthigh)))), shading interp;
print -dpng highpassffthighspac.png
surfl(fftshift(real(ifft2(highboostfft)))), shading interp;
print -dpng highboostfftspac.png
surfl(fftshift(real(ifft2(lowpassfftlow)))), shading interp;
print -dpng lowpassfftlowspac.png
surfl(fftshift(real(ifft2(highpassfftlow)))), shading interp;
print -dpng highpassfftlowspac.png

newlowpassffthigh  = lowpassffthigh.*imfft;
newhighpassffthigh = highpassffthigh.*imfft;
newhighboostfft    = highboostfft.*imfft;
newlowpassfftlow   = lowpassfftlow.*imfft;
newhighpassfftlow  = highpassfftlow.*imfft;

imwritesc((real(ifft2(newlowpassffthigh))), 'newlowpassffthigh.png');
imwritesc((real(ifft2(newhighpassffthigh))), 'newhighpassffthigh.png');
imwritesc((real(ifft2(newhighboostfft))), 'newhighboostfft.png');
imwritesc((real(ifft2(newlowpassfftlow))), 'newlowpassfftlow.png');
imwritesc((real(ifft2(newhighpassfftlow))), 'newhighpassfftlow.png');

imwritesc(im, 'im.png');

'Black-spot' filtering

Listing of blackspot.m

% BLACKSPOT
%
% Function returns a high-pass Butterworth filter centred at position
% (xc,yc) in an image
%
% usage: f = blackspot(im, cutoff, n, xc, yc)
% 
% where: im      is the image for which the filter is to be used on
%        cutoff  is the cut off frequency of the filter 0 - 0.5
%        n       is the order of the filter, the higher n is the sharper
%                the transition is
%        xc,yc   is the desired centre of the filter
function f = blackspot(im, cutoff, n, xc, yc)
    [rows, cols] = size(im);
    
    if cutoff < 0 | cutoff > 0.5
    error('cutoff frequency must be between 0 and 0.5');
    end
    
    if rem(n,1) ~= 0 | n < 1
    error('n must be an integer >= 1');
    end
    
    % X and Y matrices with ranges normalised to +/- 0.5
    x =  (ones(rows,1) * [1:cols]  - (fix(xc)))/cols;
    y =  ([1:rows]' * ones(1,cols) - (fix(yc)))/rows;
    
    radius = sqrt(x.^2 + y.^2);        % A matrix with every pixel = radius relative to centre.
    f
    = 1.0 - ( 1 ./ (1.0 + (radius ./ cutoff).^(2*n)) );   % The filter

Listing of editsect.m

% EDITSPECT -  Remove periodic interference patterns in an image.
%
% This function allows one to edit the amplitude spectrum of an image by
% 'blacking out' points in the spectrum with the mouse.  
%
% Usage:  newim = editspect(im, cutoff,n)
%
% Arguments:   im      - The image to be processed.
%              cutoff  - The radius of the blackout spot generated by a mouse click.
%                        (A typical value is in the range 0.02 - 0.1)
%              n       - order of the Butterworth function used to construct the spot.
%
% Returns:  newim      - The image reconstructed with the new amplitude
%                        spectrum.
function newim = editspect(im, cutoff, n)    

    [rows, cols] = size(im);
    
    % Calculate the FFT of the image and quadrant shift it..
    imfft = fftshift(fft2(im));
    % Display the log of the magnitude of the FFT.
    imagesc(log(abs(imfft)+eps)), colormap(gray);
    
    % While loop that allows one to repeatedly digitise points in
    % the image of the amplitude spectrum blacking out points as we go.

    but = 1;
    while but==1
        [xc,yc,but] = ginput(1);
        
        % Generate a 'blackspot' filter centred on xc,yc
        blackspotfft = blackspot(im, cutoff, n, xc, yc);
        imfft = blackspotfft.*imfft;
        blackspotfft = blackspot(imfft, cutoff, n, cols - xc, rows - yc);
        imfft = blackspotfft.*imfft;
        imagesc(log(abs(imfft)+eps)), colormap(gray);    
    end  

    newim = real(ifft2(fftshift(imfft)));

enhancing of finger3

enhancing of pidgie

Inverse Filtering

Listing of wienfilt.m

% WIENFILT
%
% Usage:  newim = wienfilt(im, length, width, ang, order, K)
%
% Arguments:   im      - The image to be processed.
%              length  - The length of the point spread function to use.
%              width   - The width of the PSF
%              ang     - angle of the PSF
%              order   - order of the Butterworth function used to construct
%                        the point spread function. 
%              K       - The estimated noise/signal power ratio.
%
% Returns:  newim      - The reconstructed image

function newim = wienfilt(im, length, width, ang, order, K)

    sqrness = 2;
    
    h = psf2(size(im),order, ang, length, width, 2);
    
    hfft = fft2(fftshift(h));
    
    imfft = fft2(im);
    
    htmp = abs(hfft).^2;
    
    newimfft = imfft.*(1./hfft).*(htmp ./ (htmp + K));
    
    newim = real(ifft2(newimfft));

enhancing of blur

enhancing of motion_blurred

Original image motion_blurred.jpg

After using wiener.m wienfilt(im, 33 , 1, 0.402 , 30, 0.02)

Hence the number plate readsN443-JJ0